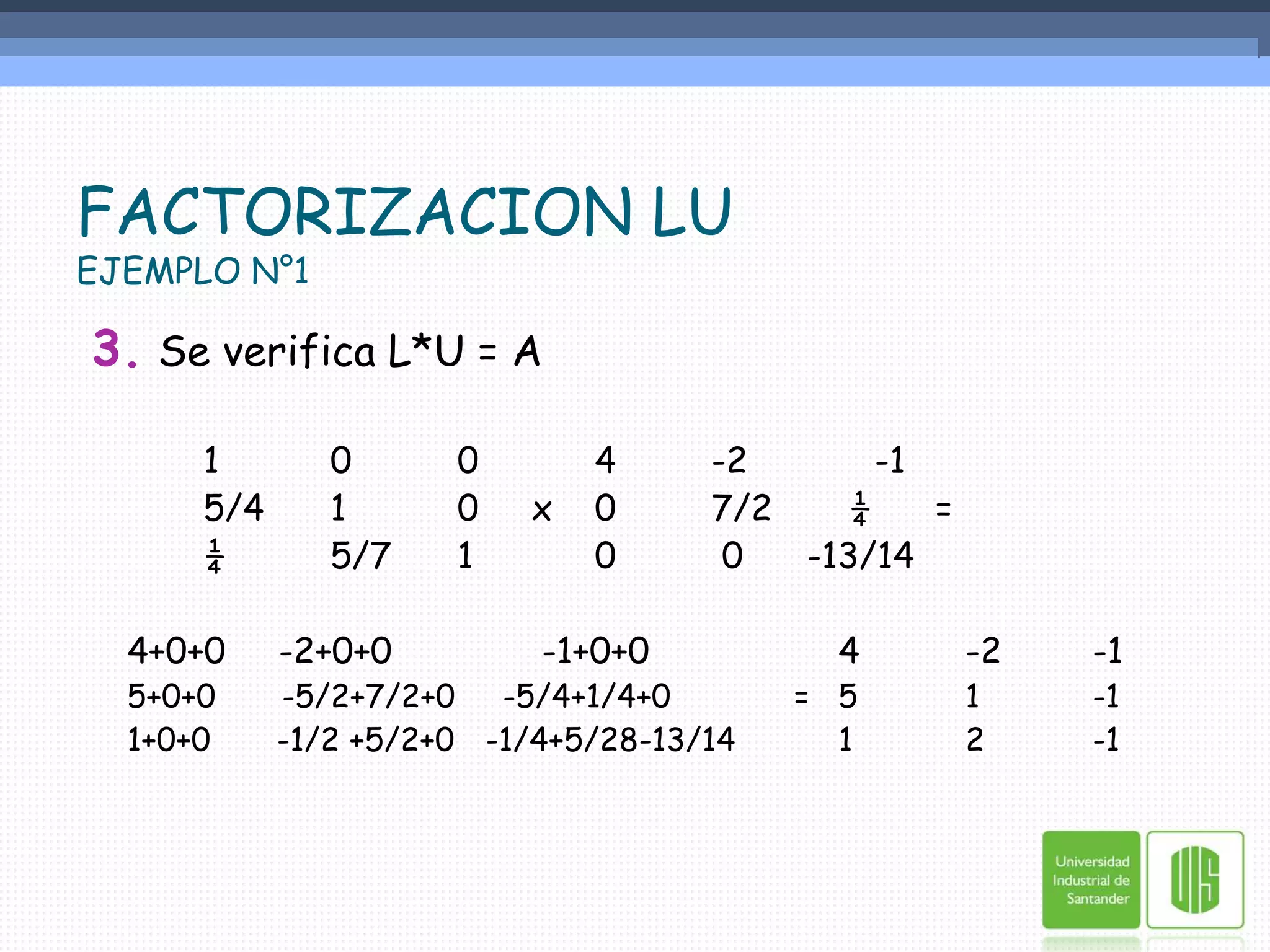
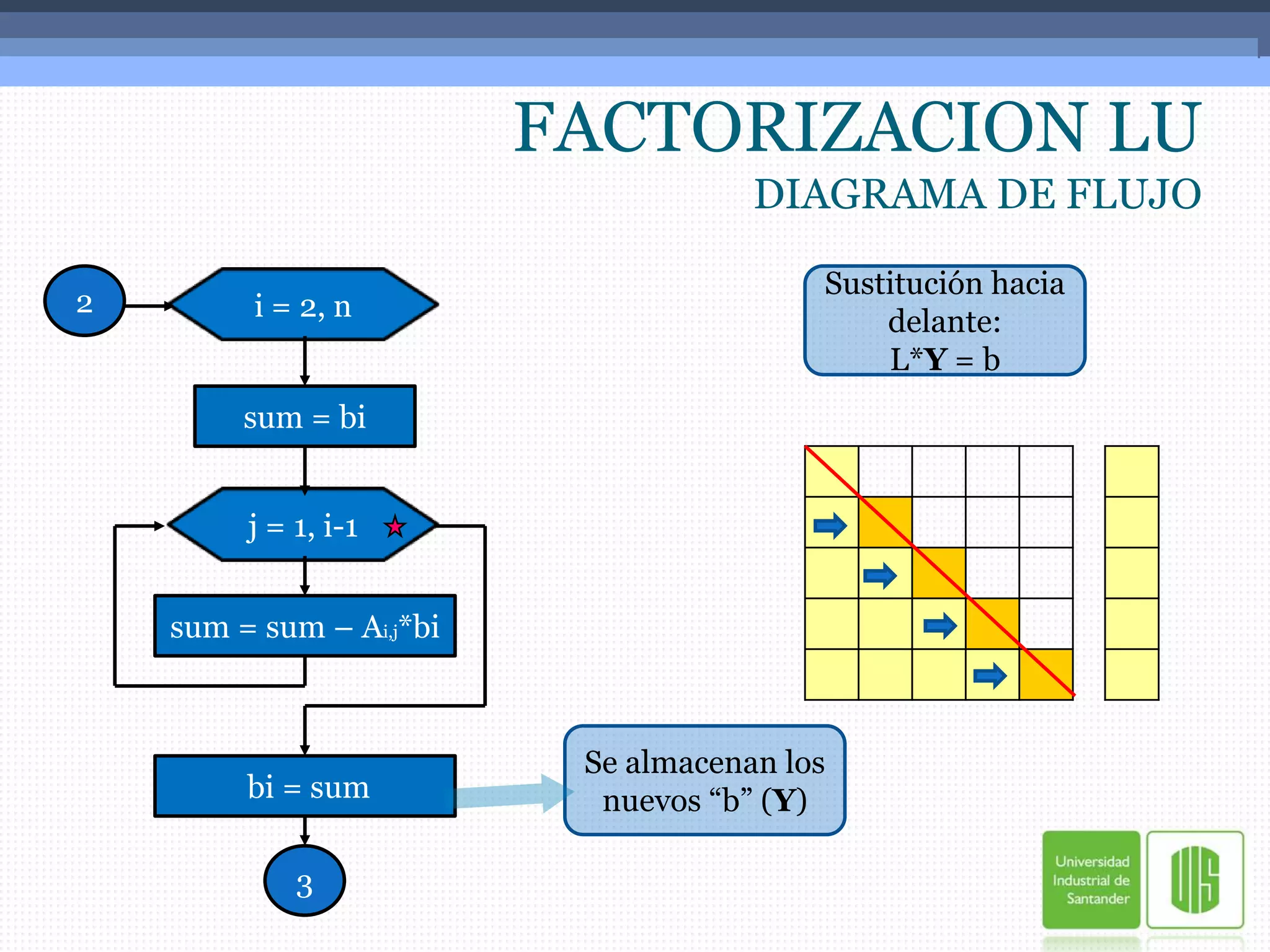
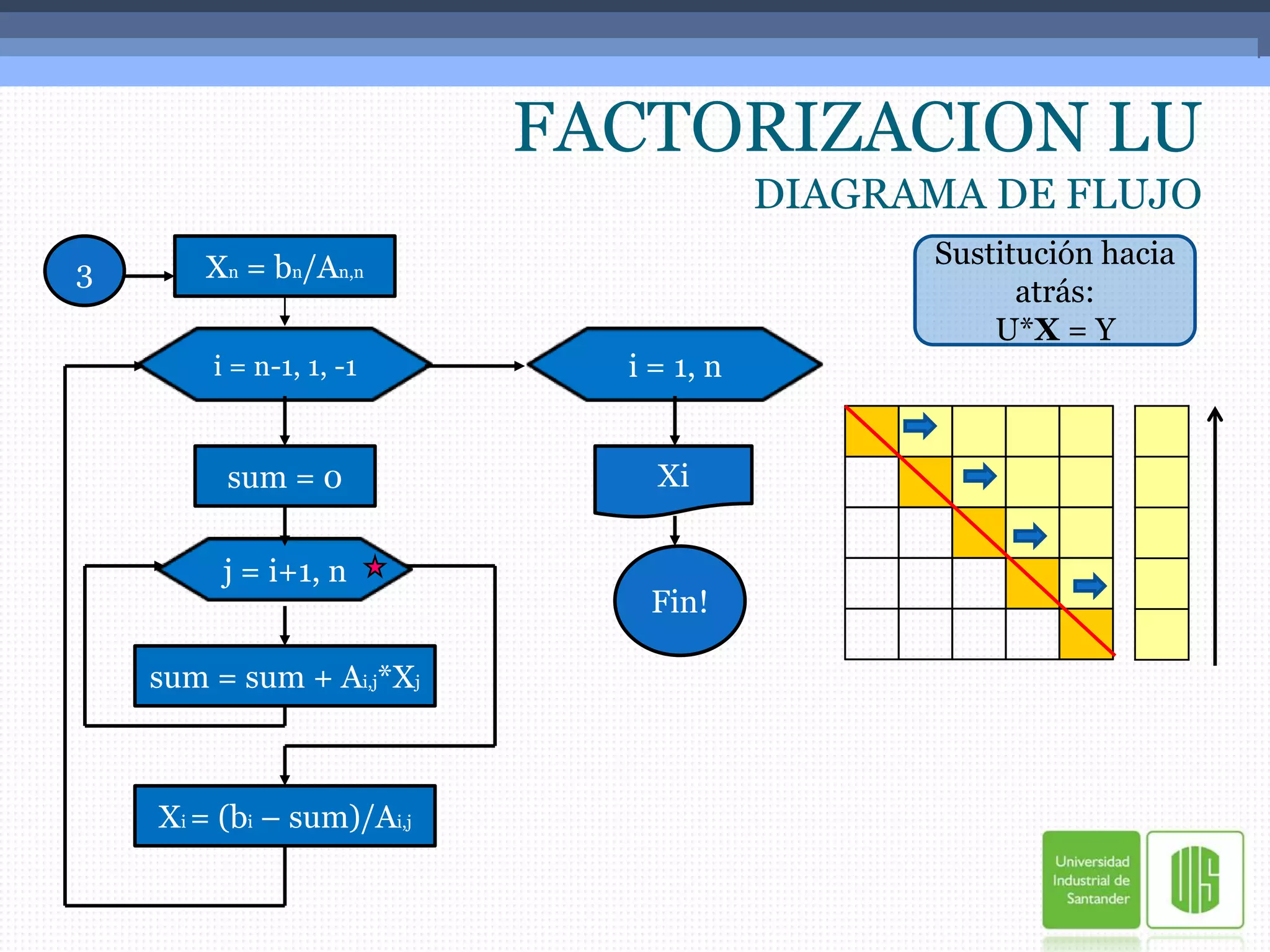
La descomposición LU es un método numérico para resolver sistemas de ecuaciones lineales. Consiste en descomponer la matriz original A en el producto de una matriz triangular inferior L y una matriz triangular superior U. Esto permite resolver el sistema en dos etapas: primero resolviendo Ly=b para encontrar y, y luego resolviendo Ux=y para encontrar x, las incógnitas del sistema. El documento explica este método y provee dos ejemplos numéricos para ilustrar los pasos.

1. LU PARA RESOLVER SISTEMAS DE ECUACIONESMÉTODOS NUMERICOSCYNDY ARGOTEJONATHAN CELISJONATHAN PEREZJHONATAN QUINTEROLINA MARGARITA GOMEZ

2. INTRODUCCION

3. DESCOMPOSICION LU Su nombre se deriva de las palabras inglesas “Lower" y “Upper”. Estudiando el proceso que se sigue en la descomposición LU es posible comprender el por qué de este nombre, analizando cómo una matriz original se descompone en dos matrices triangulares, una superior y otra inferior.

4. PASOS PARA RESOLVER UN SISTEMA DE ECUACIONES POR EL MÉTODO DE DESCOMPOSICIÓN LUObtener la matriz triangular inferior “L” y la matriz triangular superior “U”. Resolver Ly = b (para encontrar y). El resultado del paso anterior se guarda en una matriz nueva de nombre “y”.Realizar Ux = y (para encontrar x). El resultado del paso anterior se almacena en una matriz nueva llamada “x”, la cual brinda los valores correspondientes a las incógnitas de la ecuación.

5. OBTENER LA MATRIZ TRIANGULAR INFERIOR “L” Y LA MATRIZ TRIANGULAR SUPERIOR “U”

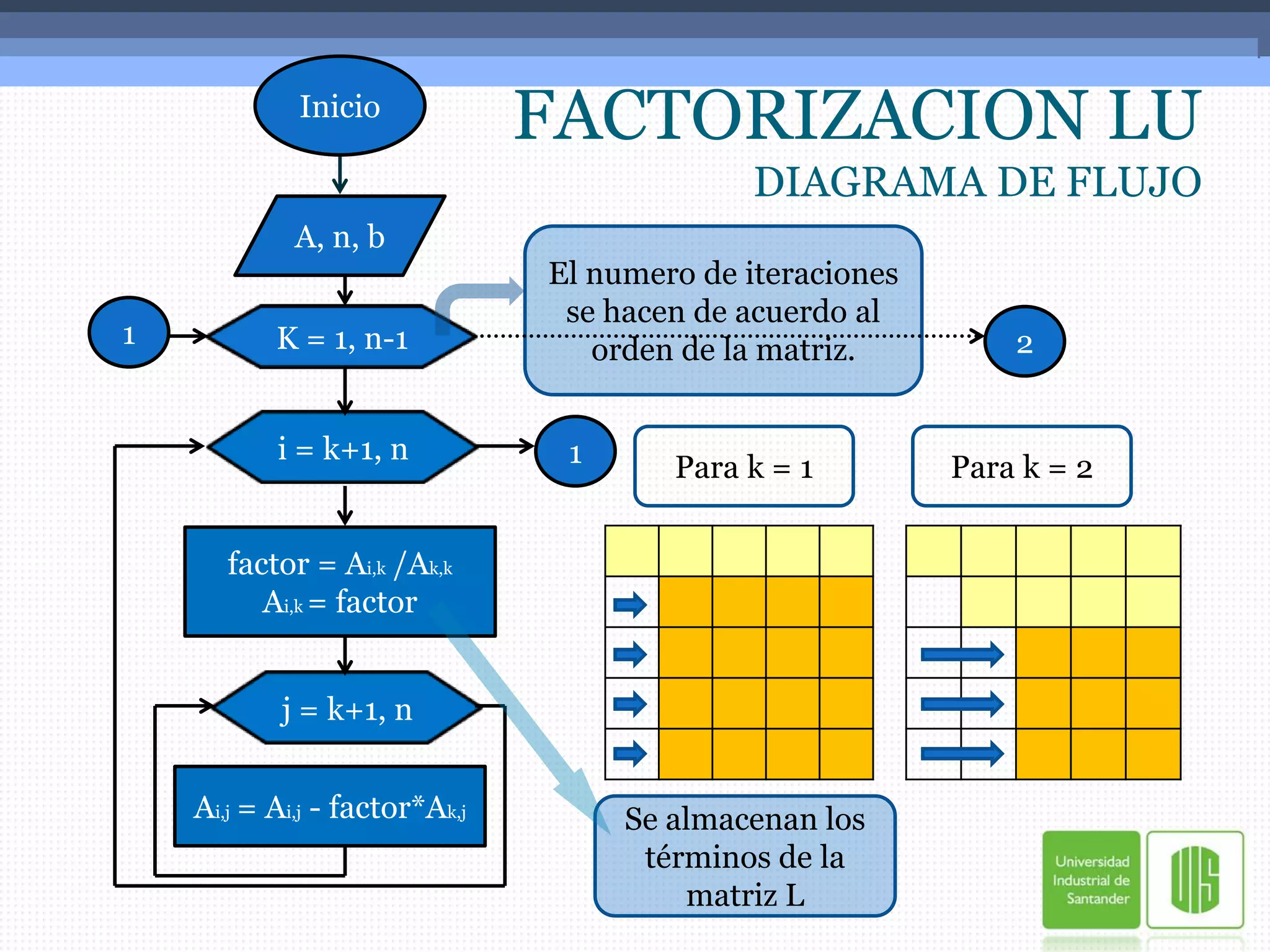
6. PASOS PARA ENCONTRAR LA MATRIZ TRIANGULAR SUPERIOR (MATRIZ [U])Hacer cero todos los valores abajo del pivote sin convertir este en 1.Para lograr lo anterior se requiere obtener un factor el cual es necesario para convertir a cero los valores abajo del pivote.Dicho factor es igual al número que se desea convertir en cero entre el número pivote.Este factor multiplicado por -1 se multiplica luego por el pivote y a ese resultado se le suma el valor que se encuentra en la posición a cambiar (el valor en la posición que se convertirá en cero).

7. PASOS PARA ENCONTRAR LA MATRIZ TRIANGULAR INFERIOR (MATRIZ [L])Construir una matriz de igual orden que la matriz original con unos en la diagonal principal y ceros para los elementos que cumplan j > i.Como los elementos debajo de la diagonal principal se ubican el múltiplo de Gauss usado en la descomposición para conseguir el “cero” en la posición correspondiente.

8. FACTORIZACION LUEJEMPLO N°1Encontrar los valores de x1, x2 y x3 para el siguiente sistema de ecuaciones: 4X1 -2X2 -X3 = 9 5X1 +X2 -X3 = 7 X1 +2X2 -X3 = 12 4 -2 -1 9 A = 5 1 -1 b = 7 1 2 -1 12

9. FACTORIZACION LUEJEMPLO N°1SOLUCION1. Se halla “U”: 4 -2 -1 5 1 -1 R2 R2 – (5/4)*R1 1 2 -1 R3 R3 – (1/4)*R1 4 -2 -1 0 7/2 ¼ 0 5/2 -3/4 R3 R3 – (5/2)/(7/2)*R2

10. FACTORIZACION LUEJEMPLO N°1SOLUCION1.Se halla “U”: 4 -2 -1 U = 0 7/2 ¼ 0 0 -13/14 2. Se halla “L”: 1 0 0 1 0 0 L = ? 1 0 L = 5/4 1 0 ? ? 1 ¼ 5/7 1

11. FACTORIZACION LUEJEMPLO N°1 3.Se verifica L*U = A 1 0 0 4 -2 -1 5/4 1 0 x 0 7/2 ¼ = ¼ 5/7 1 0 0 -13/14 4+0+0 -2+0+0 -1+0+0 4 -2 -1 5+0+0 -5/2+7/2+0 -5/4+1/4+0 = 5 1 -1 1+0+0 -1/2 +5/2+0 -1/4+5/28-13/14 1 2 -1

12. FACTORIZACION LUEJEMPLO N°14. Se despeja “Y” de L*Y = b 1 0 0 Y1 95/4 1 0 * Y2 = 7 ¼ 5/7 1 Y3 12Y1 = 9 Y1 = 95/4Y1 + Y2 = 7 Y2 = -17/41/4Y1 + 5/7Y2 +Y3 = 12 Y3 = 179/14

13. FACTORIZACION LUEJEMPLO N°15. Se despeja “X” de U*X = Y 4 -2 -1 X1 9 0 14/4 ¼ * X2 = -17/4 0 0 -13/14 X3 179/14 4X1 -2X2 -X3 = 9 X1 = -17/13 14/4X2 +1/4X3 = -17/4 X2 = -3/13 -13/14X3 = 179/14 X3 = -179/13

14. FACTORIZACION LUEJEMPLO N°2Encontrar los valores de x1, x2 y x3 para el siguiente sistema de ecuaciones: 11X1 -3X2 -2X3 = 18 5X1 -2X2 -8X3 = 13 4X1 -7X2 +2X3 = 2 11 -3 -2 18 A = 5 -2 -8 b = 13 4 -7 2 2

15. FACTORIZACION LUEJEMPLO N°2SOLUCION1. Se halla “U”: 11 -3 -2 5 -2 -8 R2 R2 – (5/11)*R1 4 -7 2 R3 R3 – (4/11)*R1 11 -3 -2 0 -7/11 -78/11 0 -65/11 30/11 R3 R3 – (-65/11)/(-7/11)*R2

16. FACTORIZACION LUEJEMPLO N°2 SOLUCION1.Se halla “U”: 11 -3 -2 U = 0 -7/11 -78/11 0 0 480/7 2. Se halla “L”: 1 0 0 1 0 0 L = ? 1 0 L = 5/11 1 0 ? ? 1 4/11 65/7 1

17. FACTORIZACION LUEJEMPLO N°2SOLUCION3.Se verifica L*U = A 1 0 0 11 -3 -2 5/11 1 0 x 0 -7/11 -78/11 = 4/11 65/7 1 0 0 480/711+0+0 -3+0+0 -2+0+0 = 11 -3 -2 5+0+0 -15/11-7/11+0 -10/11-78/11+0 = 5 -2 -8 4+0+0 -12/11 -65/11+0 -8/11+5070/77+480/7 = 4 -7 2

18. FACTORIZACION LUEJEMPLO N°2SOLUCION4. Se despeja “Y” de L*Y = b 1 0 0 Y1 185/11 1 0 * Y2 = 13 4/11 65/7 1 Y3 2Y1 = 18 Y1 = 185/11Y1 + Y2 = 13 Y2 = 53/114/11Y1 + 65/7Y2 +Y3 = 2 Y3 = -345/7

19. FACTORIZACION LUEJEMPLO N°2SOLUCION5. Se despeja “X” de U*X = Y 11 -3 -2 X1 18 0 -7/11 -78/11 * X2 = 53/11 0 0 480/7 X3 -345/7 11X1 -3X2 -2X3 =18 X1 = 13/8 -7/11X2 -78/11X3 = 53/11 X2 = 7/16 480/7X3 = -345/7 X3 = -23/32

20. FACTORIZACION LUDIAGRAMA DE FLUJOInicioA, n, b El numero de iteraciones se hacen de acuerdo al orden de la matriz.12K = 1, n-1i = k+1, n1Para k = 1Para k = 2factor = Ai,k/Ak,kAi,k = factorj = k+1, nAi,j= Ai,j - factor*Ak,jSe almacenan los términos de la matriz L

21. FACTORIZACION LUDIAGRAMA DE FLUJO2Sustitución hacia delante:L*Y = bi = 2, nsum = bij = 1, i-1sum = sum – Ai,j*biSe almacenan los nuevos “b” (Y) bi= sum3

22. FACTORIZACION LUDIAGRAMA DE FLUJOSustitución hacia atrás:U*X = Y3Xn = bn/An,ni = n-1, 1, -1i = 1, nsum = 0Xij = i+1, nFin!sum = sum + Ai,j*XjXi = (bi – sum)/Ai,j

23. FACTORIZACION LUReferencias de consultahttp://www.unizar.es/aragon_tres/unidad6/Matrices/u6matte20.pdfhttp://www.ditutor.com/matrices/matriz_simetrica.htmlhttp://www.cramster.com/reference/wii.aspx?wiki_name=Band_matrixChapra, Steven; Canale, Raymond. Métodos númericos para ingenieros. 3ra Edición. Mc Graw Hill 2000.